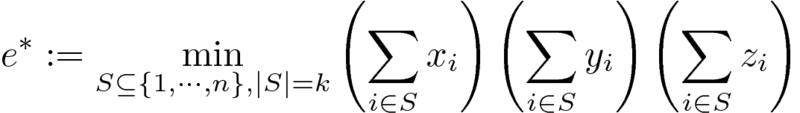ACM-ICPC 2014 アジア地区東京大会 J

ACM-ICPC 2014 アジア地区東京大会

J: Exhibition

問題
fを求めよ。

n, k, A, B, C, x_i, y_i, z_iは入力の定数。

解法
解説上がってたのでそっち読んだほうがいい。

こういう問題は数式で考えるのがいいのか、空間幾何で考えるのがいいのかよくわからない。

2段階に分けると
(1) e*を求める
(2) 画像の添字集合Tを列挙してそれぞれfを求める

(1), (2)に共通して言えるが添字集合S, Tは実際には添字を保つ必要はなく、せいぜいx,y,zのそれぞれの和のtupleがあれば良い。
このtupleを3次元空間の座標と考えてe = xyzのeを最小値を求めるので、このtupleの凸包の頂点で、原点側にある頂点が解の候補となる。
これらはnCkよりずっと少ない。

凸包の頂点を列挙するためにe*を和の式で考えたい。
e*を最小化する添字集合Sを一つ取ってS'とするとS'に依存して何かしらのスカラーP,Q,Rを定数とするとS'は次のe** (e*とは値が異なる) も最小化する。

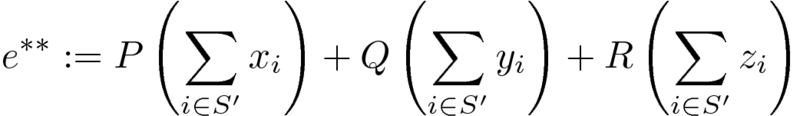
P,Q,Rは例えば

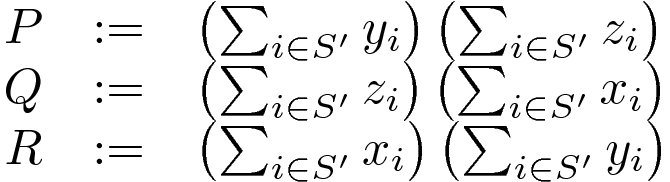
がある。
P,Q,Rが先に決まっていればP x_i + Q y_i + R z_i = e_iでソートすることでS'が求まる。
これはN個の平行な平面Px + Qy + Rz = e_iを下側から順に並べる感覚。

平面は3点で決まるので試すべき平面はN^3個。
選んだ3点がソートすると連続して並ぶようになる。
この平面を原点まで落として、平面からの距離でソートすれば良い。
頂点が2以下の時や、平面ができない場合のために法線(1,1,1)の平面も試すべき？
よってSの候補とTの候補を求めるのは3点組合せとソートでO(N^4 log N)、
nth_element使えばO(N^4)でできると思う。

(1) S全部調べてe*が求まる。
(2) 各Tについて、(x_1, y_1, z_1)を入れてe*にしつつfを最小化する。
αβγ空間の[0,1]^3の立方体の中で、平面fをずらすと[0,1]^3の辺上で最適な交点を持つ。二次の図で例になるか。

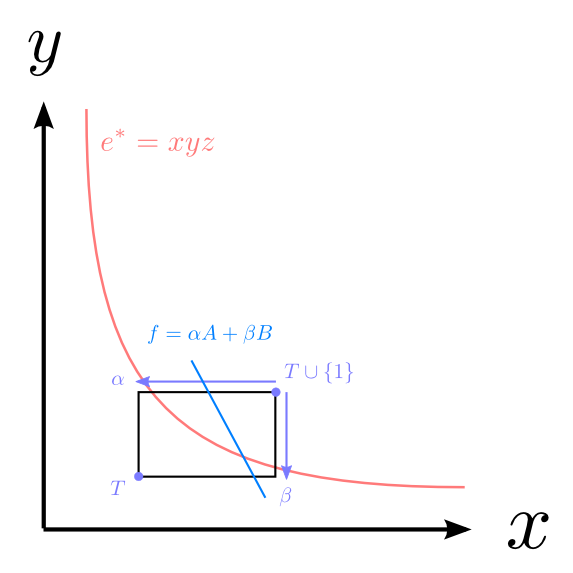
図中の長方形は横x_1、縦y_1であるが、αβ空間では正方形に当たる。
αβγを動かすとfが動き、fはαβγ空間の原点に近いほうが小さい値を取る。

#include<cstdio>
#include<iostream>
#include<vector>
#include<algorithm>
#include<string>
#include<cstring>
#include<map>
#include<cmath>
#include<set>
using namespace std;

typedef long long LL;

#define y1 MY_y1

#define REP(i, n) for(int i=0; i<int(n); i++)
#define EACH(i,c) for(__typeof((c).begin()) i=(c).begin();i!=(c).end();i++)

template<class T> inline T &amin(T &a, const T &b) { if (a>b) a=b; return a; }
template<class T> inline T &amax(T &a, const T &b) { if (a<b) a=b; return a; }


const double INF = 1e12;
const double EPS = 1e-9;

const int G[2][4] = { {0, 0, 1, 1},
		      {0, 1, 0, 1},
};

bool LE(double x, double y) {
    return x <= y + EPS;
}

int N, K;
int A, B, C;
int x[55], y[55], z[55];

double E, ans;

double X, Y, Z;
int x1, y1, z1;
vector<int> Xv, Yv, Zv;


void update(double X_t, double Y_t, double Z_t) {
    double a = 1 - (X_t - X) / x1;
    double b = 1 - (Y_t - Y) / y1;
    double c = 1 - (Z_t - Z) / z1;

    if (LE(0, a) && LE(a, 1) && LE(0, b) && LE(b, 1) && LE(0, c) && LE(c, 1)) 
	amin(ans, A*a + B*b + C*c);
}


// plane OA * s + OB * t
// normal vector OC
double OA[3], OB[3], OC[3];

// square of distance point_i and plane (OA, OB)
double area(int i) {
    return pow(OC[0] * x[i] + OC[1] * y[i] + OC[2] * z[i], 2);
}
bool ord(int i, int j) {
    return area(i) < area(j);
}

// index set
int I[55];

void calc() {
    REP (t, N) I[t] = t;

    // choose K-1 products from N-1 products
    sort(I+1, I+N, ord);
    int xx = 0, yy = 0, zz = 0;

    for (int t=1; t<K; t++) {
	xx += x[I[t]];
	yy += y[I[t]];
	zz += z[I[t]];
    }
    Xv.push_back(xx);
    Yv.push_back(yy);
    Zv.push_back(zz);

    // choose K product from N products, and minimize E
    sort(I, I+N, ord);
    xx = yy = zz = 0;
    REP (t, K) {
	xx += x[I[t]];
	yy += y[I[t]];
	zz += z[I[t]];
    }
    amin(E, (double)xx * yy * zz);
}


int main() {
    scanf("%d%d%d%d%d", &N, &K, &A, &B, &C);
    REP (i, N) scanf("%d%d%d", x+i, y+i, z+i);

    if (N == 1) {
	puts("0.000000");
	return 0;
    }

    x1 = x[0];
    y1 = y[0];
    z1 = z[0];

    E = 1e60;
    ans = 1e60;

    OC[0] = OC[1] = OC[2] = 1;
    calc();

    REP (i, N) {
	REP (j, N) {
	    REP (k, N) {
		OA[0] = x[j] - x[i] + EPS;
		OA[1] = y[j] - y[i] + EPS;
		OA[2] = z[j] - z[i] + EPS;

		OB[0] = x[k] - x[i] + EPS + EPS;
		OB[1] = y[k] - y[i] + EPS + EPS;
		OB[2] = z[k] - z[i] + EPS + EPS;

		OC[0] = OA[1] * OB[2] - OA[2] * OB[1];
		OC[1] = OA[2] * OB[0] - OA[0] * OB[2];
		OC[2] = OA[0] * OB[1] - OA[1] * OB[0];

		calc();
	    }
	}
    }

    REP (i, Xv.size()) {
	X = Xv[i];
	Y = Yv[i];
	Z = Zv[i];
	
	if (double(X) * Y * Z > E) continue;
	
	for (int d=0; d<4; d++) {
	    double X_t, Y_t, Z_t;
	    X_t = X + G[0][d] * x1; Y_t = Y + G[1][d] * y1;
	    if (X_t > EPS && Y_t > EPS) {
		Z_t = E / X_t / Y_t;
		update(X_t, Y_t, Z_t);
	    }
	    
	    X_t = X + G[0][d] * x1; Z_t = Z + G[1][d] * z1;
	    if (X_t > EPS && Z_t > EPS) {
		Y_t = E / X_t / Z_t;
		update(X_t, Y_t, Z_t);
	    }
	    
	    Y_t = Y + G[0][d] * y1; Z_t = Z + G[1][d] * z1;
	    if (Y_t > EPS && Z_t > EPS) {
		X_t = E / Y_t / Z_t;
		update(X_t, Y_t, Z_t);
	    }
	}
    }

    printf("%.9f\n", ans);

    return 0;
}

別解
三次元幾何とかやりたくない。凸包とか知らない。x_iが整数で小さいことを利用してDPで解きたい。

map<pair<int, int>, int> dp[50][51];
dp[i][j][(x,y)] = i番目までのj個使って(x,y)の時のzの最小値;

これはiを消して使いまわしてもAOJでMLEした。

キーを減らさなければならない。xは全て取るとして(y,z)を減らす。
二次平面上の点集合Xについて、Xの部分集合{p | p in X, Xのp以外のどの点qもpの左下にない}をXの前線と呼ぶことにする。
図のピンクの頂点に相当。

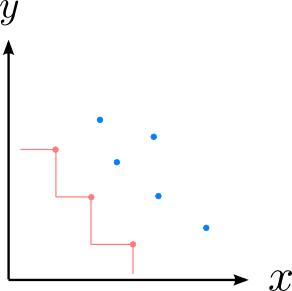
2013年アジア地区会津大会で出たやつだ。

set<pair<int,int> > dp[50][51][5001];
dp[i][j][x] = i番目までのj個使ってxの時の(y,z)の前線;

頂点数は凸包より多くなるが、少なくとも凸包の頂点を含んでいる。
この前線を解の候補とするとメモリも間に合い解ける。
ソースコード中ではiを使いまわして節約している。

#include<cstdio>
#include<iostream>
#include<vector>
#include<algorithm>
#include<string>
#include<cstring>
#include<map>
#include<cmath>
#include<set>
using namespace std;

typedef long long LL;

#define y1 MY_Y1

#define REP(i, n) for(int i=0; i<int(n); i++)
#define EACH(i,c) for(__typeof((c).begin()) i=(c).begin();i!=(c).end();i++)

template<class T> inline T &amin(T &a, const T &b) { if (a>b) a=b; return a; }
template<class T> inline T &amax(T &a, const T &b) { if (a<b) a=b; return a; }


const double INF = 1e12;
const double EPS = 1e-9;

const int G[2][4] = { {0, 0, 1, 1},
		      {0, 1, 0, 1},
};

bool LE(double x, double y) {
    return x <= y + EPS;
}

int N, K;
int A, B, C;
int x[55], y[55], z[55];

double E, ans;


set<pair<int,int> > dp[51][5001], T[5001];

double X, Y, Z;
int x1, y1, z1;

void insert(set<pair<int, int> > &s, pair<int, int> p) {
    set<pair<int, int> >::iterator it = s.lower_bound(p);
    while (it != s.end() && p.second <= it->second) s.erase(it++);
    if (it != s.begin() && p.second >= (--it)->second) return;
    s.insert(p);
}

void update(double X_t, double Y_t, double Z_t) {
    double a = 1 - (X_t - X) / x1;
    double b = 1 - (Y_t - Y) / y1;
    double c = 1 - (Z_t - Z) / z1;

    if (LE(0, a) && LE(a, 1) && LE(0, b) && LE(b, 1) && LE(0, c) && LE(c, 1)) 
	amin(ans, A*a + B*b + C*c);
}

int main() {
    scanf("%d%d%d%d%d", &N, &K, &A, &B, &C);
    REP (i, N) scanf("%d%d%d", x+i, y+i, z+i);
    x1 = x[0];
    y1 = y[0];
    z1 = z[0];

    // (x[0], y[0], z[0]) の代わりに (x[N-1], y[N-1], z[N-1])をproduct 1とする
    swap(x[0], x[N-1]);
    swap(y[0], y[N-1]);
    swap(z[0], z[N-1]);

    dp[0][0].insert(make_pair(0, 0));

    REP (i, N) {
	if (i == N-1)
	    REP (xx, 5001) T[xx] = dp[K-1][xx];
	
	for (int j=i; j>=0; j--) {
	    for (int xx = 5000; xx>=0; xx--) {
		EACH (e, dp[j][xx]) {
		    pair<int, int> p(e->first + y[i], e->second + z[i]);
		    insert(dp[j+1][xx+x[i]], p);
		}
	    }
	}

    }

    E = 1e60;

    for (int xx=0; xx<5001; xx++) {
	EACH (e, dp[K][xx]) {
	    double yy = e->first, zz = e->second;
	    amin(E, (double)xx * yy * zz);
	}
    }

    ans = 1e60;

    for (int xx=0; xx<5001; xx++) {
	EACH (e, T[xx]) {
	    X = xx;
	    Y = e->first;
	    Z = e->second;

	    if (double(X) * Y * Z > E) continue;
	    
	    
	    for (int d=0; d<4; d++) {
		double X_t, Y_t, Z_t;
		X_t = X + G[0][d] * x1; Y_t = Y + G[1][d] * y1;
		if (X_t > EPS && Y_t > EPS) {
		    Z_t = E / X_t / Y_t;
		    update(X_t, Y_t, Z_t);
		}
		
		X_t = X + G[0][d] * x1; Z_t = Z + G[1][d] * z1;
		if (X_t > EPS && Z_t > EPS) {
		    Y_t = E / X_t / Z_t;
		    update(X_t, Y_t, Z_t);
		}
		
		Y_t = Y + G[0][d] * y1; Z_t = Z + G[1][d] * z1;
		if (Y_t > EPS && Z_t > EPS) {
		    X_t = E / Y_t / Z_t;
		    update(X_t, Y_t, Z_t);
		}
	    }
	}
    }
    printf("%.9f\n", ans);

    return 0;
}